n头奶牛开车,第i头速度上限为si,高速上有m个车道,如果在一头奶牛前面有d头奶牛位于它所在车道,这头奶牛的实际速度为si-k*d,高速最低速度为l,求一共可以让多少头奶牛上高速。n,m≤50000
先让所有奶牛按速度上限排序,然后依次选取:求出当前奶牛前面最多可以有多少头奶牛x,然后二分求出m条车道中当前奶牛数小于等于x且最大的那条车道,把这头奶牛放入这个车道;如果没位置可放或这头奶牛速度上限小于l,就将它弃置。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 50100
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,d,l,a[maxn],b[maxn],ans;
int find(int x){
int l=1,r=m,ans=-1;
while(l<=r){int mid=(l+r)>>1; if(x>=b[mid])ans=mid,r=mid-1;else l=mid+1;}
return ans;
}
int main(){
n=read(); m=read(); d=read(); l=read(); inc(i,1,n)a[i]=read(); sort(a+1,a+1+n);
inc(i,1,n){
if(a[i]<l)continue; int c=(a[i]-l)/d,e=find(c); if(e==-1)continue;else b[e]++,ans++;
}
printf("%d",ans); return 0;
}n行m列的草地上有一些位置有障碍物。第0时刻奶牛在(r1,c1),第t时刻奶牛在(r2,c2)(注意这里都是行在前,列在后),求奶牛走的方案数。n,m≤100,t≤15。
dp。f[i][j][k]表示当前为第i时刻,在j行k列,则f[i][j][k]=f[i+1][j-1][k]+f[i+1][j+1][k]+f[i+1][j][k-1]+f[i+1][j][k+1],前提是这些位置不出边界且不为障碍物。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 110
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define dec(i,j,k) for(int i=j;i>=k;i--)
using namespace std;
int n,m,t,x[maxn][maxn],y[maxn][maxn],x1,y1,x2,y2; char map[maxn][maxn];
int main(){
scanf("%d%d%d",&n,&m,&t); inc(i,1,n)scanf("%s",map[i]+1); scanf("%d%d%d%d",&x1,&y1,&x2,&y2); x[x2][y2]=1;
dec(i,t,1){
memset(y,0,sizeof(y));
inc(j,1,n)inc(k,1,m){
if(j+1<=n&&map[j+1][k]!='*')y[j][k]+=x[j+1][k];
if(j-1>=1&&map[j-1][k]!='*')y[j][k]+=x[j-1][k];
if(k+1<=m&&map[j][k+1]!='*')y[j][k]+=x[j][k+1];
if(k-1>=1&&map[j][k-1]!='*')y[j][k]+=x[j][k-1];
}
swap(x,y);
}
printf("%d",x[x1][y1]); return 0;
}m个挤奶时间段,每个时间段有一个产奶量,每次产完奶奶牛要休息r分钟,问最多产多少奶。m≤1000,时间≤1000000。
类似bzoj1664,方程改为f[i]=max(f[i+1],f[range[j].r+range[j].value],j为时刻i开始的产奶时间段)。然而本弱的写法时间和空间复杂度都排倒数,神犇们都是用背包dp的写法(我不会)QAQ
#include <cstdio>
#include <algorithm>
#include <cstring>
#define maxn 1010
#define ll long long
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct rg{int r; ll w; int n;}; rg rgs[maxn]; ll f[maxn*2000]; int n,m,r,g[maxn*1000],mx;
int main(){
n=read(); m=read(); r=read();
inc(i,1,m){int a=read(),b=read(),c=read(); rgs[i]=(rg){b,c,g[a]}; g[a]=i; mx=max(mx,a);}
for(int i=mx;i>=0;i--){
f[i]=f[i+1]; for(int j=g[i];j;j=rgs[j].n)f[i]=max(f[i],f[rgs[j].r+r]+rgs[j].w);
}
printf("%lld",f[0]); return 0;
}数轴上,起点在n,终点在k,每次走可以向左走一步或向右走一步或瞬移到当前坐标的两倍位置,问最少走几次。0≤n,k≤100000。
bfs,允许走的位置边界为[0,max(n,k)+1]。下界为0原因是如果走到小于0的位置,k≥0,则瞬移和往左走都是南辕北辙,只能向右走,那么一开始就不应该走到小于0的位置导致浪费时间。上界为max(n,k)+1的原因是如果你走到了大于这个数的位置,k必定小于当前位置,则你必须一步一步的往回走,而这样做显然比之前就别走到这个位置花更多时间……(我承认我乱扯一通)所以复杂度为100000。
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <queue>
#define maxn 100100
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
queue <int> q; int tim[maxn],n,k,mx;
int main(){
scanf("%d%d",&n,&k); memset(tim,-1,sizeof(tim)); q.push(n); tim[n]=0; mx=max(n,k)+1;
while(!q.empty()){
int x=q.front(); q.pop();
if(x+1<=mx&&tim[x+1]==-1){q.push(x+1); tim[x+1]=tim[x]+1; if(x+1==k)break;}
if(x-1>=0&&tim[x-1]==-1){q.push(x-1); tim[x-1]=tim[x]+1; if(x-1==k)break;}
if(x<<1<=mx&&tim[x<<1]==-1){q.push(x<<1),tim[x<<1]=tim[x]+1; if(x<<1==k)break;}
}
printf("%d",tim[k]); return 0;
}求两个数的和,每个数绝对值≤10(107)。
又用Python水过了……
给一个带权有向图,和一个源点,求往返源点最短距离最长的点往返源点的最短距离。
正插边做spfa,倒着插边再做一次spfa。两次最短路之和最大值为所求。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1010
#define INF 0x3ffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,w,n;}; e es[maxn*100]; int g[maxn],ess;
void pe(int f,int t,int w){es[++ess]=(e){t,w,g[f]}; g[f]=ess;}
int d[maxn],sm[maxn],f[maxn*100],t[maxn*100],w[maxn*100],n,m,s; bool inq[maxn];
queue <int> q;
void spfa(){
while(!q.empty())q.pop(); memset(inq,0,sizeof(inq)); inc(i,1,n)d[i]=INF;
q.push(s); inq[s]=1; d[s]=0;
while(!q.empty()){
int x=q.front(); q.pop(); inq[x]=0;
for(int i=g[x];i;i=es[i].n)if(d[x]+es[i].w<d[es[i].t]){
d[es[i].t]=d[x]+es[i].w;
if(!inq[es[i].t])inq[es[i].t]=1,q.push(es[i].t);
}
}
}
int main(){
n=read(); m=read(); s=read(); inc(i,1,m)f[i]=read(),t[i]=read(),w[i]=read();
ess=0; memset(g,0,sizeof(g)); inc(i,1,m)pe(f[i],t[i],w[i]); spfa(); inc(i,1,n)sm[i]+=d[i];
ess=0; memset(g,0,sizeof(g)); inc(i,1,m)pe(t[i],f[i],w[i]); spfa(); inc(i,1,n)sm[i]+=d[i];
int ans=0; inc(i,1,n)ans=max(ans,sm[i]); printf("%d",ans); return 0;
}给个点集,求无向有权图中点集里的哪些点到点1的距离小于等于M。点集内点数≤100,图中点数≤500,边数≤1000。
spfa。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 510
#define INF 0x3ffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,w,n;}; e es[maxn*4]; int g[maxn],ess;
void pe(int f,int t,int w){
es[++ess]=(e){t,w,g[f]}; g[f]=ess; es[++ess]=(e){f,w,g[t]}; g[t]=ess;
}
int d[maxn],f,p,c,m,cow[maxn],tot; bool inq[maxn];
queue <int> q;
void spfa(){
while(!q.empty())q.pop(); memset(inq,0,sizeof(inq)); inc(i,1,f)d[i]=INF;
q.push(1); inq[1]=1; d[1]=0;
while(!q.empty()){
int x=q.front(); q.pop(); inq[x]=0;
for(int i=g[x];i;i=es[i].n)if(d[x]+es[i].w<d[es[i].t]){
d[es[i].t]=d[x]+es[i].w;
if(!inq[es[i].t])inq[es[i].t]=1,q.push(es[i].t);
}
}
}
int main(){
f=read(); p=read(); c=read(); m=read(); inc(i,1,p){int x=read(),y=read(),z=read(); pe(x,y,z);}
inc(i,1,c)cow[i]=read(); spfa(); inc(i,1,c)if(d[cow[i]]<=m)tot++; printf("%d\n",tot);
inc(i,1,c)if(d[cow[i]]<=m)printf("%d\n",i); return 0;
}一个人和n牛渡河,人载i头牛渡河所需时间为m+sigma(j,1,i)a[j],人不载牛所需时间为m,到了对岸如果还要载牛必须花时间m把船开回来。问最短时间。n≤2500
dp。f[i][j]=min(f[i+1][j+1]+a[j+1],f[i+1][0]+a[j+1]+m*2),最后答案为f[1][0]+m。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 3000
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define dec(i,j,k) for(int i=j;i>=k;i--)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,a[maxn],x[maxn],y[maxn];
int main(){
n=read(); m=read(); inc(i,1,n)a[i]=read();
dec(i,n,1){
memset(y,0,sizeof(y)); inc(j,0,i)y[j]=min(x[j+1]+a[j+1],x[0]+a[j+1]+m*2); swap(x,y);
}
printf("%d",x[0]+m); return 0;
}求按点1-a1-a2…-an-n走的最短路长度是多少。点数小于等于100。
floyd。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 110
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int map[maxn][maxn],a[maxn*100],n,m,ans;
int main(){
n=read(); m=read(); inc(i,1,m)a[i]=read(); inc(i,1,n)inc(j,1,n)map[i][j]=read();
inc(k,1,n)inc(i,1,n)inc(j,1,n)if(map[i][k]+map[k][j]<map[i][j])map[i][j]=map[i][k]+map[k][j];
ans+=map[1][a[1]]; inc(i,2,m)ans+=map[a[i-1]][a[i]]; ans+=map[a[m]][n]; printf("%d",ans); return 0;
}给一个序列a,令ci=ai+1到an第一个比ai大的位置j与i的距离。求sigma(i,1,n)ci。
用一个递减的单调栈维护。注意最后答案要开long long。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 80100
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a[maxn],x[maxn],y[maxn],sz; long long ans;
int main(){
n=read(); for(int i=1;i<=n;i++)a[i]=read(); x[0]=0x3fffffff; y[0]=n+1; sz=0;
for(int i=n;i>=1;i--){while(a[i]>x[sz])sz--; ans+=(y[sz]-i-1); x[++sz]=a[i]; y[sz]=i;}
printf("%lld",ans); return 0;
}给出一个N,使用一些2的若干次幂的数相加来求之.问有多少种方法。N≤1000000。
可以写完全背包,然而排名会倒数~正解是一个递推式:
f[i]=f[i-1],当i为奇数,f[1]=1
f[i]=f[i-1]+f[i/2],当i为偶数
神犇们的证明我没看懂QAQ。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1000001
#define mod 1000000000
using namespace std;
int n,f[maxn];
int main(){
scanf("%d",&n); f[1]=1;
inc(i,2,n){f[i]=f[i-1]; if(!(i&1))f[i]=(f[i]+f[i>>1])%mod;}
printf("%d",f[n]); return 0;
}对于字符串S的前i个字符构成的子串,既是它的后缀同时又是它的前缀,并且该后缀与该前缀不重叠,将这种字符串的数量记作num[i]。给出字符串S求所有num[i]+1的乘积模1000000007。字符串长度≤1000000
先求一遍fail函数,得到数组记为next1,然后再求next2数组,表示满足next1[j]*2≤i的next1[j],这一过程也是可以递推的。同时用cnt数组记录next1[j]有多少个。num[i]就是cnt[next2[i]]。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 1000100
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define mod 1000000007
using namespace std;
char s[maxn]; int next1[maxn],next2[maxn],cnt[maxn],t,len; long long ans;
int main(){
scanf("%d",&t);
while(t--){
scanf("%s",s+1); len=strlen(s+1); next1[1]=0; cnt[1]=1; next2[1]=0;
inc(i,2,len){
int j=next1[i-1]; while(j&&s[j+1]!=s[i])j=next1[j];
if(s[j+1]==s[i])next1[i]=j+1,cnt[i]=cnt[next1[i]]+1;else next1[i]=0,cnt[i]=1;
}
inc(i,2,len){
int j=next2[i-1]; if(j*2+2>i)j=next1[j]; while(j&&s[j+1]!=s[i])j=next1[j];
if(s[j+1]==s[i])next2[i]=j+1;else next2[i]=0;
}
ans=1; inc(i,1,len)ans=ans*(cnt[next2[i]]+1)%mod; printf("%lld\n",ans);
}
return 0;
}n个砝码,每个砝码重量大于前两个砝码质量和,天平承重为c,求天平上最多可放多种的砝码。n≤1000,c≤2^30。
斐波那契数列到30多项就爆int了,所以本题n其实≤30。故爆搜即可,加个剪枝:当前选的砝码质量和+剩下砝码质量和仍≤ans就返回。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a[maxn],c,ans; long long sm[maxn];
void dfs(int x,int y){
if(sm[x]+y<=ans)return; ans=max(ans,y); for(int i=x;i>=1;i--)if(y+a[i]<=c)dfs(i-1,y+a[i]);
}
int main(){
n=read(); c=read();
inc(i,1,n)a[i]=read(),sm[i]=sm[i-1]+a[i]; while(a[n]>c)n--; dfs(n,0); printf("%d",ans);
}n头奶牛,每头一个身高和音量。每头牛的音量会被左边离它最近的比它高的和右边离它最近的比它高的牛听到。问牛听到的最大音量。n≤50000
单调栈维护牛的身高递减。左右各做一次,累加求解。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define dec(i,j,k) for(int i=j;i>=k;i--)
#define maxn 50100
using namespace std;
int s1[maxn],s2[maxn],h[maxn],vol[maxn],ss,n,ans[maxn];
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int main(){
n=read(); inc(i,1,n)h[i]=read(),vol[i]=read();
s1[1]=h[1]; s2[1]=1; ss=1;
inc(i,2,n){while(ss&&s1[ss]<h[i])ss--; if(ss)ans[s2[ss]]+=vol[i]; s1[++ss]=h[i]; s2[ss]=i;}
s1[1]=h[n]; s2[1]=n; ss=1;
dec(i,n-1,1){while(ss&&s1[ss]<h[i])ss--; if(ss)ans[s2[ss]]+=vol[i]; s1[++ss]=h[i]; s2[ss]=i;}
inc(i,1,n)ans[0]=max(ans[0],ans[i]); printf("%d",ans[0]); return 0;
}N点M边有向图,每个入度为0的点都有无限只奶牛,现在它们要回宿舍(点1),求通过量最大的路的通过量。N≤5000,M≤50000
一条路的通过量=到达节点到入度为0节点的方案数*点1到出发节点的方案数(其实我也不知道为什么,这题意完全是模糊的),2次dfs就行了。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define dec(i,j,k) for(int i=j;i>=k;i--)
#define maxn 5010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int f1[maxn],f2[maxn],n,m,f[maxn*10],t[maxn*10];
struct e{int t,n;}; e es[maxn*10]; int g[maxn];
int dfs1(int x){
if(f1[x])return f1[x];
if(!g[x])f1[x]=1;else{
for(int i=g[x];i;i=es[i].n){f1[x]+=dfs1(es[i].t);}
}
return f1[x];
}
int dfs2(int x){
if(f2[x])return f2[x];
if(!g[x])f2[x]=1;else{
for(int i=g[x];i;i=es[i].n){f2[x]+=dfs2(es[i].t);}
}
return f2[x];
}
int main(){
n=read(); m=read(); inc(i,1,m)f[i]=read(),t[i]=read();
memset(g,0,sizeof(g)); inc(i,1,m)es[i]=(e){f[i],g[t[i]]},g[t[i]]=i; dfs1(n);
memset(g,0,sizeof(g)); inc(i,1,m)es[i]=(e){t[i],g[f[i]]},g[f[i]]=i; inc(i,1,n)if(!f2[i])dfs2(i);
inc(i,1,m)f1[0]=max(f1[0],f1[f[i]]*f2[t[i]]);
printf("%d",f1[0]); return 0;
}n个月,每月有一个酸奶需求量(吨)和酸奶成本(元每吨)。酸奶可以保存,费用为S(元每月每吨),求最小总费用。n≤10000
第i月每吨酸奶的成本为Cj+s*(i-j),j∈[1,i],化简得Cj-s*j+s*i,因为s*i只和当前相关,所以维护一个最小的Cj-s*j即可。注意开long long。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,s,mn; long long ans;
int main(){
n=read(); s=read();
inc(i,1,n){
int a=read(),b=read(); if(i==1)mn=a-s*i;else mn=min(mn,a-s*i); ans+=(mn+s*i)*b;
}
printf("%lld",ans); return 0;
}询问区间最大值减区间最小值的差。序列大小≤50000
RMQ问题。注意log2区间长度可先递推好,这样可以保证询问O(1)。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 50100
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,a[maxn],lg[maxn],mx[maxn][20],mn[maxn][20];
int main(){
n=read(); m=read(); inc(i,1,n)a[i]=read();
inc(i,1,n)mx[i][0]=a[i],mn[i][0]=a[i];
for(int i=0;1<<i<=n;i++)lg[1<<i]=i; inc(i,1,n)if(!lg[i])lg[i]=lg[i-1];
for(int i=1;1<<i<=n;i++)inc(j,1,n)if(j+(1<<i)-1<=n)
mx[j][i]=max(mx[j][i-1],mx[j+(1<<(i-1))][i-1]),mn[j][i]=min(mn[j][i-1],mn[j+(1<<(i-1))][i-1]);
inc(i,1,m){
int a=read(),b=read(),c=lg[b-a+1];
printf("%d\n",max(mx[a][c],mx[b-(1<<c)+1][c])-min(mn[a][c],mn[b-(1<<c)+1][c]));
}
return 0;
}n只牛在啃花,第i只每分钟啃ai朵,赶走它需要2*bi分钟,问最少会被啃掉多少朵。n≤100000
贪心。只考虑第i只牛与第j只牛孰先孰后,如果第i只牛先会多啃掉2biaj朵,第j只牛先会被啃掉2aibj朵,因此按这个排序就行了。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct nd{int t,d,id;}; nd nds[maxn]; int n,sm; long long ans;
bool cmp(nd a,nd b){return a.t*b.d<b.t*a.d;}
int main(){
n=read(); inc(i,1,n)nds[i].t=read(),nds[i].d=read(),nds[i].id=i; sort(nds+1,nds+1+n,cmp);
for(int i=n;i>=1;i--)ans+=sm*nds[i].t*2,sm+=nds[i].d;
printf("%lld",ans); return 0;
}求最长单调递增子序列,序列大小≤5000
蒟蒻弱写了一个O(n^2)的。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 5100
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn],f[maxn],n;
int main(){
n=read(); inc(i,1,n)a[i]=read();
inc(i,1,n){
f[i]=1; inc(j,1,i-1)if(a[j]<a[i])f[i]=max(f[i],f[j]+1);
}
inc(i,1,n)f[0]=max(f[0],f[i]); printf("%d",f[0]); return 0;
}n点m边有向图,每次给出询问x,y求x到y路径中最大边权的最小值是多少。n≤500
floyd变形。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 310
#define INF 0x3fffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,t,g[maxn][maxn];
int main(){
n=read(); m=read(); t=read(); inc(i,1,n)inc(j,1,n)g[i][j]=INF;
inc(i,1,m){int a=read(),b=read(); g[a][b]=read();}
inc(k,1,n)inc(i,1,n)inc(j,1,n)g[i][j]=min(g[i][j],max(g[i][k],g[k][j]));
inc(i,1,t){int a=read(),b=read(); printf("%d\n",g[a][b]==INF?-1:g[a][b]);}
return 0;
}n头牛在不同坐标处吃草,没有牛相邻。求一个没有牛的点到所有点曼哈顿距离和最小和这样点的个数。n≤10000
先求x坐标的中位数区间,再求y坐标的中位数区间,如果n为偶数,答案为这个二维区间点数-落在这个区间里的牛数。n为奇数,且这个中位数点有牛的话,就在这个点的上下左右调整,然后找距离和最小的点和这样点的个数。情况比较多,容易WA。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 10100
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct p{int x,y;}; p ps[maxn]; int lx,rx,ly,ry,n,tot,ans;
bool cmp1(p a,p b){return a.x<b.x;}
bool cmp2(p a,p b){return a.y<b.y;}
int main(){
n=read(); inc(i,1,n)ps[i].x=read(),ps[i].y=read();
sort(ps+1,ps+n+1,cmp1);
if(n&1)lx=rx=ps[(n>>1)+1].x;else lx=ps[n>>1].x,rx=ps[(n>>1)+1].x;
sort(ps+1,ps+n+1,cmp2);
if(n&1)ly=ry=ps[(n>>1)+1].y;else ly=ps[n>>1].y,ry=ps[(n>>1)+1].y;
tot=(rx-lx+1)*(ry-ly+1); inc(i,1,n)if(ps[i].x>=lx&&ps[i].x<=rx&&ps[i].y>=ly&&ps[i].y<=ry)tot--;
if(!tot){
int a[4]={0,0,0,0}; tot=0; ans=0x3fffffff;
lx++; inc(i,1,n)a[0]+=abs(lx-ps[i].x)+abs(ly-ps[i].y); ans=min(a[0],ans); lx--;
lx--; inc(i,1,n)a[1]+=abs(lx-ps[i].x)+abs(ly-ps[i].y); ans=min(a[1],ans); lx++;
ly++; inc(i,1,n)a[2]+=abs(lx-ps[i].x)+abs(ly-ps[i].y); ans=min(a[2],ans); ly--;
ly--; inc(i,1,n)a[3]+=abs(lx-ps[i].x)+abs(ly-ps[i].y); ans=min(a[3],ans); ly++;
inc(i,0,3)if(ans==a[i])tot++;
}else{inc(i,1,n)ans+=abs(lx-ps[i].x)+abs(ly-ps[i].y);}
printf("%d %d",ans,tot); return 0;
}n只牛,牛结成群当且仅当两只牛曼哈顿距离≤c或存在第三头牛使两头牛与它的曼哈顿距离都≤c,求最大的群和群数。n≤100000
好神啊。先把曼哈顿距离转成切比雪夫距离,(x,y)转为(x+y,x-y)。然后按x坐标排序,用两个指针维护使x坐标差值≤c,同时将新插入的y坐标放入set,每次在set里查找出与当前y差值不超过c的最大y,将这两个点合并成一个集合,用并查集维护。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100100
#define INF 0x3fffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct p{int x,y;}; p ps[maxn];
bool cmp(p a,p b){return a.x==b.x?a.y<b.y:a.x<b.x;}
struct data{
int id,v;
bool operator < (const data &a)const{return v==a.v?id<a.id:v<a.v;}
};
set<data> s; int n,c,l,fa[maxn],cnt[maxn];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void merge(int _x,int _y){int x=find(_x),y=find(_y); if(x!=y)fa[y]=x;}
int main(){
n=read(),c=read(); inc(i,1,n){int a=read(),b=read(); ps[i]=(p){a+b,a-b};} sort(ps+1,ps+1+n,cmp);
s.clear(); s.insert((data){0,INF}); s.insert((data){0,-INF});
l=1; s.insert((data){1,ps[1].y}); inc(i,1,n)fa[i]=i;
inc(i,2,n){
while(ps[i].x-ps[l].x>c)s.erase(s.find((data){l,ps[l].y})),l++;
set<data>::iterator x=s.lower_bound((data){0,ps[i].y}),y=x; y--;
if(x->v-ps[i].y<=c)merge(i,x->id); if(ps[i].y-y->v<=c)merge(i,y->id);
s.insert((data){i,ps[i].y});
}
inc(i,1,n)cnt[find(i)]++; int ans=0; inc(i,1,n)if(cnt[i])ans++; printf("%d ",ans);
ans=0; inc(i,1,n)ans=max(ans,cnt[i]); printf("%d",ans); return 0;
}每头牛都喜欢几种食品和饮料,现在每种食品和饮料都有一个,问最多能使多少头牛同时获得喜欢的食品和饮料。牛数、饮料数、食品数≤500
最大流,源向所有食品连边,食品向被喜欢的牛连边,牛向喜欢的饮料连边,饮料向汇连边,流量都为1。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 10000
#define INF 0x3fffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,c,n;}; e es[maxn*2]; int g[maxn],ess;
void pe(int f,int t,int c){
es[++ess]=(e){t,c,g[f]}; g[f]=ess; es[++ess]=(e){f,0,g[t]}; g[t]=ess;
}
void init(){memset(g,-1,sizeof(g)); ess=-1;}
queue<int>q; int h[maxn];
bool bfs(int s,int t){
while(!q.empty())q.pop(); memset(h,-1,sizeof(h)); h[s]=0; q.push(s);
while(!q.empty()){
int x=q.front(); q.pop();
for(int i=g[x];i!=-1;i=es[i].n)if(es[i].c&&h[es[i].t]==-1)h[es[i].t]=h[x]+1,q.push(es[i].t);
}
return h[t]!=-1;
}
int dfs(int x,int t,int f){
if(x==t)return f; int u=0;
for(int i=g[x];i!=-1;i=es[i].n)if(es[i].c&&h[es[i].t]==h[x]+1){
int w=dfs(es[i].t,t,min(f,es[i].c)); f-=w; u+=w; es[i].c-=w; es[i^1].c+=w; if(!f)return u;
}
if(!u)h[x]=-1; return u;
}
int dinic(int s,int t){int flow=0; while(bfs(s,t))flow+=dfs(s,t,INF); return flow;}
int n,f,d,s,t;
int main(){
n=read(); f=read(); d=read(); s=0; t=f+n*2+d+1; init();
inc(i,1,n){
pe(f+i,f+n+i,1);
int a=read(),b=read();
inc(j,1,a){int c=read(); pe(c,f+i,1);}
inc(j,1,b){int c=read(); pe(f+n+i,f+n*2+c,1);}
}
inc(i,1,f)pe(s,i,1); inc(i,1,d)pe(f+n*2+i,t,1); printf("%d",dinic(s,t)); return 0;
}草坪上有N个水龙头,修剪两个水管费用为欧几里得距离的平方。 修水管的人只愿意修费用大于等于c的水管,问将水龙头联通的最小总费用。N≤2000
最小生成树。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 2010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int x[maxn],y[maxn],n,c,fa[maxn],cnt,ans;
struct e{int f,t,w;}; e es[maxn*maxn]; int ess;
inline bool cmp(const e& a,const e& b){return a.w<b.w;}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
inline int sqr(int x){return x*x;}
int main(){
n=read(); c=read(); inc(i,1,n)x[i]=read(),y[i]=read();
inc(i,1,n)inc(j,i+1,n){int a=sqr(x[i]-x[j])+sqr(y[i]-y[j]); if(a>=c)es[++ess]=(e){i,j,a};}
sort(es+1,es+1+ess,cmp); inc(i,1,n)fa[i]=i;
inc(i,1,ess){
int x=find(es[i].f),y=find(es[i].t); if(x!=y)fa[y]=x,cnt++,ans+=es[i].w;
if(cnt==n-1)break;
}
if(cnt==n-1)printf("%d",ans);else printf("-1"); return 0;
}K只奶牛分散在N个牧场,问多少地点是所有奶牛都可到达的地方。n≤1000
倒插边然后对每个点dfs,如果经过的奶牛为k则累计答案。注意可能有多只牛在同个牧场,要用数组记录。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,n;}; e es[maxn*10]; int g[maxn],ess;
void pe(int f,int t){es[++ess]=(e){t,g[f]}; g[f]=ess;}
bool cow[maxn],vis[maxn]; int ans,tot,k,n,m,cnt;
void dfs(int x){
if(cow[x])tot++; for(int i=g[x];i;i=es[i].n)if(!vis[es[i].t])vis[es[i].t]=1,dfs(es[i].t);
}
int main(){
k=read(),n=read(),m=read();
inc(i,1,k){int a=read(); cow[a]=1;} inc(i,1,m){int a=read(),b=read(); pe(b,a);}
k=0; inc(i,1,n)if(cow[i])k++;
inc(i,1,n){
memset(vis,0,sizeof(vis)); vis[i]=1; tot=0; dfs(i); if(tot==k)ans++;
}
printf("%d",ans); return 0;
}最大生成树。
最大生成树。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 25010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a[maxn],b[maxn],x,y,ans;
int main(){
n=read(); x=read(); y=read(); inc(i,1,n)a[i]=read(),b[i]=read();
sort(a+1,a+n+1); sort(b+1,b+n+1);
inc(i,1,n)if(b[i]>a[i])ans+=(b[i]-a[i])*x;else ans+=(a[i]-b[i])*y;
printf("%d",ans); return 0;
}给个序列a,再给个可变换顺序的序列b,求a变为b的最小代价。a增加一个单位代价为x,降低一个单位代价为y。序列大小≤25000
a,b排序,直接统计即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 25010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a[maxn],b[maxn],x,y,ans;
int main(){
n=read(); x=read(); y=read(); inc(i,1,n)a[i]=read(),b[i]=read();
sort(a+1,a+n+1); sort(b+1,b+n+1);
inc(i,1,n)if(b[i]>a[i])ans+=(b[i]-a[i])*x;else ans+=(a[i]-b[i])*y;
printf("%d",ans); return 0;
}维护数据结构支持合并和弹出最小值。n≤1000000,m≤100000
可并堆,注意本题合并时要判断两个节点是否在同一个堆中。本弱写了左偏树和斜堆,发现斜堆比左偏树快,不知道为什么,求神犇解答。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1000010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int ch[maxn][2],v[maxn],fa[maxn]; bool die[maxn];
int find(int x){while(fa[x])x=fa[x]; return x;}
int merge(int x,int y){
if(!x||!y)return x+y; if(v[x]>v[y])swap(x,y); ch[x][1]=merge(ch[x][1],y);
fa[ch[x][1]]=x; swap(ch[x][0],ch[x][1]); return x;
}
void pop(int x){
fa[ch[x][0]]=fa[ch[x][1]]=0; merge(ch[x][0],ch[x][1]); ch[x][0]=ch[x][1]=0;
}
int n,m; char opt[3];
int main(){
n=read(); inc(i,1,n)v[i]=read(); m=read();
inc(i,1,m){
scanf("%s",opt);
if(opt[0]=='M'){
int a=read(),b=read(); if(die[a]||die[b])continue; int aa=find(a),bb=find(b);
if(aa==bb)continue; merge(aa,bb);
}
if(opt[0]=='K'){
int a=read(); if(die[a]||a>n)puts("0");else{
int aa=find(a); pop(aa); die[aa]=1; printf("%d\n",v[aa]);
}
}
}
return 0;
}n个区间,求最多的区间集合使其互不覆盖。n≤50000
好像是第三次出现这种题了~但是区间范围可达10^9,不能dp了QAQ膜了一发题解发现只要按区间右端点排序然后贪心取即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 50100
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct nd{int l,r;} nds[maxn];
inline bool cmp(const nd &a,const nd &b){return a.r<b.r;}
int n,r,ans;
int main(){
n=read(); inc(i,1,n){int a=read(),b=read(); nds[i]=(nd){a,b};}
sort(nds+1,nds+1+n,cmp);
inc(i,1,n){
if(nds[i].l>=r)ans++,r=nds[i].r;
}
printf("%d",ans); return 0;
}给出abcdefghi,求2a+2b+2c+2d+2e+2f+2g+2h+i。a~h≤60,i≤2^63
发现只有极限数据才会爆unsigned long long,所以先让i-1,然后把它们累加起来,发现这个数据是极限数据就手算出2^64输出字符串,否则就直接+1即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
unsigned long long a[10]; int t;
int main(){
scanf("%d",&t);
while(t--){
inc(i,0,8)scanf("%llu",&a[i]); a[9]=0;
if(a[8]==0){
inc(i,0,7)a[9]+=(1LL<<a[i]); printf("%llu\n",a[9]);
}else{
a[8]--; inc(i,0,7)a[9]+=(1LL<<a[i]); a[9]+=a[8];
if(a[9]==18446744073709551615)printf("18446744073709551616\n");else printf("%llu\n",a[9]+1);
}
}
return 0;
}给定玩家一个有2n个元素的栈,这些元素拥有n个不同的编号,每个编号正好有两个元素。玩家每次可以交换两个相邻的元素。如果在交换之后,两个相邻的元素编号相同,则将他们都从栈中移除,所有在他们上面的元素都会掉落下来并且可以导致连锁反应。求最少的步数将方块全部消除。
用一个栈维护,如果遇到一个没有遇到过的编号就入栈,否则就让之前的那个元素出栈,两个元素之间的元素向下移一位,并将两个元素的距离计入答案。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int st[maxn],top,ans,n; bool in[maxn];
int main(){
n=read();
inc(i,1,2*n){
int x=read();
if(!in[x])in[x]=1,st[++top]=x;else{
int j=top; while(st[j]!=x)j--; inc(k,j,top-1)st[k]=st[k+1],ans++; top--; in[x]=0;
}
}
printf("%d",ans); return 0;
}维护一个序列,支持移动元素,查询元素是第几个,查询第k个元素编号。
可以用treap和splay,我写的是splay。移动元素就是先删一个节点在将这个节点插入到对应位置,注意各种分操作(如splay、find)的次序性。反思:本弱又WA又T,最后自己造了一个极限数据发现死循环了,对着大数据调了半天才发现是分操作次序不当导致错误。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 80100
using namespace std;
int ch[maxn][2],fa[maxn],v[maxn],sz[maxn],pos[maxn],root,book[maxn],tot,n,m;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();};
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
inline void update(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1;}
void rotate(int x){
if(!x||!fa[x])return; int a=fa[x],b=fa[fa[x]]; bool c=x==ch[fa[x]][1],d=a==ch[fa[a]][1];
if(b)ch[b][d]=x; fa[x]=b; ch[a][c]=ch[x][!c]; if(ch[x][!c])fa[ch[x][!c]]=a; ch[x][!c]=a; fa[a]=x;
update(a); update(x); if(b)update(b);
}
void splay(int x,int y){
if(x==y)return; int z=fa[y];
while(fa[x]!=z){
if(fa[x]!=y)(x==ch[fa[x]][1])^(fa[x]==ch[fa[fa[x]]][1])?rotate(x):rotate(fa[x]);
rotate(x);
}
if(root==y)root=x;
}
void build(int x,int l,int r){
int mid=l+r>>1; v[x]=book[mid]; pos[book[mid]]=x;
if(l<=mid-1)ch[x][0]=++tot,build(ch[x][0],l,mid-1),fa[ch[x][0]]=x;
if(mid+1<=r)ch[x][1]=++tot,build(ch[x][1],mid+1,r),fa[ch[x][1]]=x;
update(x);
}
int querynum(int x,int k){
if(k<=sz[ch[x][0]])return querynum(ch[x][0],k);
if(k==sz[ch[x][0]]+1)return x;
return querynum(ch[x][1],k-sz[ch[x][0]]-1);
}
int queryrank(int x){
splay(x,root); return sz[ch[x][0]];
}
int pre(int y){
splay(y,root); return querynum(ch[y][0],sz[ch[y][0]]);
}
int nex(int y){
splay(y,root); return querynum(ch[y][1],1);
}
void add(int x,int y,int z){
splay(y,root); splay(x,ch[root][0]); ch[x][1]=z; fa[z]=x; update(x); update(root);
}
void erase(int z){
int x=pre(z),y=nex(z); splay(y,root); splay(x,ch[root][0]); ch[x][1]=0; fa[z]=0; update(x); update(root);
}
void top(int s){
int x=pos[s]; erase(x); int y=querynum(root,1),z=nex(y); add(y,z,x);
}
void bottom(int s){
int x=pos[s]; erase(x); int y=querynum(root,sz[root]-1),z=nex(y); add(y,z,x);
}
void insert(int s,int t){
int a1=pos[s],a2=queryrank(a1)+t; erase(a1); int a3=querynum(root,a2),a4=nex(a3); add(a3,a4,a1);
}
int ask(int s){return queryrank(pos[s])-1;}
int query(int s){return v[querynum(root,s+1)];}
int main(){
n=read(); m=read(); inc(i,2,n+1)book[i]=read(); tot=root=1; build(root,1,n+2);
inc(i,1,m){
char opt[8]; scanf("%s",opt);
if(opt[0]=='T'){int a=read(); top(a);}
if(opt[0]=='B'){int a=read(); bottom(a);}
if(opt[0]=='I'){int a=read(),b=read(); insert(a,b);}
if(opt[0]=='A'){int a=read(); printf("%d\n",ask(a));}
if(opt[0]=='Q'){int a=read(); printf("%d\n",query(a));}
}
return 0;
}n个节点,1号节点已经连入互联网,现在需要将整个图连入网络。有K条边可以免费连接,最后总费用为所有连边费用的最大值,求最小总费用。n≤10000
二分费用,将连边费用大于二分值的长度记为1,否则记为0,求最短路,如果到某个点的距离超过k,则需要增加答案,继续二分。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1001
#define INF 0x3fffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,w,y,n;}; e es[maxn*20]; int ess,g[maxn];
void pe(int f,int t,int w){
es[++ess]=(e){t,0,w,g[f]}; g[f]=ess; es[++ess]=(e){f,0,w,g[t]}; g[t]=ess;
}
bool inq[maxn]; int d[maxn],n,m,k,ans; queue<int>q;
bool spfa(){
while(!q.empty())q.pop(); memset(inq,0,sizeof(inq)); inc(i,1,n)d[i]=INF;
inq[1]=1; q.push(1); d[1]=0;
while(!q.empty()){
int x=q.front(); q.pop(); inq[x]=0;
for(int i=g[x];i;i=es[i].n)if(d[es[i].t]>d[x]+es[i].w){
d[es[i].t]=d[x]+es[i].w; if(!inq[es[i].t])inq[es[i].t]=1,q.push(es[i].t);
}
}
if(d[n]>k)return 0;else return 1;
}
bool check(int x){
inc(i,1,ess)if(es[i].y<=x)es[i].w=0;else es[i].w=1;
return spfa();
}
int main(){
n=read(); m=read(); k=read(); int l=0,r=0; ans=-1;
inc(i,1,m){int a=read(),b=read(),c=read(); pe(a,b,c); r=max(r,c);}
while(l<=r){
int mid=(l+r)>>1; if(check(mid))ans=mid,r=mid-1;else l=mid+1;
}
printf("%d",ans); return 0;
}n头牛,其中有牡牛和牝牛两种,要求任意两只牡牛中要有k只牝牛,问几种方案。n≤100000
dp。f[i]表示第i头牛为牡牛的方案数,f[i]=sigma(j,1,i-k-1)f[j],这个可以用前缀和维护,最后答案为sigma(i,1,n)f[i]。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100100
#define mod 5000011
using namespace std;
int n,k,sm[maxn],f;
int main(){
scanf("%d%d",&n,&k); sm[0]=1;
inc(i,1,n){
if(i<=k)f=1;else f=sm[i-k-1];
sm[i]=(sm[i-1]+f)%mod;
}
printf("%d",sm[n]);
}n种巧克力,每种有个单价和最多能买几块,问有B块钱一共最多能买几块。n≤100000
贪心,按单价排序。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n; ll b,ans;
struct nd{ll p,c;}; nd nds[maxn];
inline bool cmp(const nd &a,const nd &b){return a.p<b.p;}
int main(){
n=read(); b=read(); inc(i,1,n)nds[i]=(nd){read(),read()}; sort(nds+1,nds+1+n,cmp);
inc(i,1,n){
ll use=min(nds[i].c,b/nds[i].p);
b-=use*nds[i].p; ans+=use; if(use!=nds[i].c)break;
}
printf("%lld",ans); return 0;
}n点m边无向图,有k头奶牛要送礼,它必须去农场(1号节点)拿礼物然后到目的地送。问每只奶牛的最短距离。n≤50000
以1号节点为源点spfa求一次最短路即可(反正是无向边)。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define ll long long
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 50010
#define INF 0x3fffffff
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,w,n;}; e es[maxn*4]; int g[maxn],ess;
void pe(int f,int t,int w){es[++ess]=(e){t,w,g[f]}; g[f]=ess; es[++ess]=(e){f,w,g[t]}; g[t]=ess;}
int n,m,b,d[maxn]; bool inq[maxn]; queue<int>q;
void spfa(){
while(!q.empty())q.pop(); memset(inq,0,sizeof(inq)); inc(i,1,n)d[i]=INF;
q.push(1); inq[1]=1; d[1]=0;
while(!q.empty()){
int x=q.front(); q.pop(); inq[x]=0;
for(int i=g[x];i;i=es[i].n)if(d[es[i].t]>d[x]+es[i].w){
d[es[i].t]=d[x]+es[i].w; if(!inq[es[i].t])q.push(es[i].t),inq[es[i].t]=1;
}
}
}
int main(){
n=read(); m=read(); b=read();
inc(i,1,m){int a=read(),b=read(),c=read(); pe(a,b,c);} spfa();
inc(i,1,b){int a=read(),b=read(); printf("%d\n",d[a]+d[b]);} return 0;
}n块巧克力,每次吃可以增加ai点快乐,每天早晨睡觉起来快乐值会减半,求如何使d天睡觉前的最小快乐值最大。n,d≤50000
二分快乐值,每天不够就吃。注意如果最后一天有剩余巧克力,必须将其全部吃完。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,d,bel[maxn]; ll h[maxn],ans1,ans2[maxn];
bool check(ll x){
ll hap=0; int p=1;
inc(i,1,d){
while(hap<x&&p<=n)hap+=h[p],bel[p]=i,p++; if(hap<x)return 0; hap>>=1;
}
while(p<=n)bel[p]=d,p++; inc(i,1,n)ans2[i]=bel[i]; ans1=x; return 1;
}
int main(){
n=read(); d=read(); inc(i,1,n)h[i]=read();
ll l=1,r=50000000000LL;
while(l<=r){
ll mid=(l+r)>>1; if(check(mid))l=mid+1;else r=mid-1;
}
printf("%lld\n",ans1); inc(i,1,n)printf("%lld\n",ans2[i]);
}n个牧场,在每个牧场见控制站的花费为ai,在该处建控制站能控制从此处到左边第一个控制站(或边界)之间的牧场。一个牧场被控制的花费等于它到控制它的控制站之间的牧场数目(不包括自身,但包括控制站所在牧场)乘上该牧场的放养量。求最小费用。
推公式:
\[ \begin{split} f[i]&=f[j]+\sum_{k=j+1}^i{(i-k)\times b[k]}+a[i] \\ &=f[j]+\sum_{k=j+1}^i{i\times b[k]-k\times b[k]}+a[i] \\ &=f[j]+\sum_{k=j+1}^i{i\times b[k]}-\sum_{k=j+1}^i{k\times b[k]}+a[i] \\ &=f[j]+i\times \sum_{k=j+1}^i{b[k]}-\sum_{k=j+1}^i{k\times b[k]}+a[i] \end{split} \]
\(\sum_{k=j+1}^i{b[k]}\)和\(\sum_{k=j+1}^i{k\times b[k]}\)可用前缀和维护,故原式\(=f[j]+i\times(sum1[i]-sum1[j])-(sum2[i]-sum2[j])+a[i]\),然后就可以斜率优化了:
\[ \begin{split} f[j]&+i\times(sum1[i]-sum1[j])-(sum2[i]-sum2[j])+a[i]< \\ &f[k]+i\times(sum1[i]-sum1[k])-(sum2[i]-sum2[k])+a[i] \\ &\Leftrightarrow f[j]-i\times sum1[j]+sum2[j]<f[k]-i*sum1[k]+sum2[k] \\ &\Leftrightarrow f[j]-f[k]+sum2[j]-sum2[k]<i\times (sum1[j]-sum1[k]) \\ &\Leftrightarrow \frac{f[j]-f[k]+sum2[j]-sum2[k]}{sum1[j]-sum1[k]}>i,\forall j<k \end{split} \]
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1000010
#define ll long long
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
ll f[maxn],sm1[maxn],sm2[maxn],a[maxn]; int n,q[maxn],l,r;
inline double calc(int j,int k){
return ((double)f[j]-f[k]+sm2[j]-sm2[k])/((double)sm1[j]-sm1[k]);
}
int main(){
n=read(); inc(i,1,n)a[i]=read();
inc(i,1,n){ll b=read(); sm1[i]=sm1[i-1]+b; sm2[i]=sm2[i-1]+b*i;} l=r=1; q[l]=0;
inc(i,1,n){
while(l<r&&calc(q[l],q[l+1])<i)l++; f[i]=f[q[l]]+i*(sm1[i]-sm1[q[l]])-sm2[i]+sm2[q[l]]+a[i];
while(l<r&&calc(q[r-1],q[r])>calc(q[r],i))r--; q[++r]=i;
}
printf("%lld",f[n]); return 0;
}给个序列,A与B轮流取数,谁取的数总和大谁赢。每次只能取序列两端,问A能取的数总和最大是多少。假设两人都用最优策略。序列大小≤5000
dp。f[i][j][0]=max(f[i+1][j][1]+a[i],f[i][j-1][1]+a[j]),f[i][j][1]=min(f[i+1][j][0],f[i][j-1][0])。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 5010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn],f[2][maxn][2],n; bool x,y;
int main(){
n=read(); inc(i,1,n)a[i]=read(); x=0; y=1;
for(int i=n;i>=1;i--){
inc(j,1,n)f[y][j][0]=f[y][j][1]=0;
inc(j,i,n){
f[y][j][0]=max(f[x][j][1]+a[i],f[y][j-1][1]+a[j]);
f[y][j][1]=min(f[x][j][0],f[y][j-1][0]);
}
swap(x,y);
}
printf("%d",f[x][n][0]); return 0;
}给定一个长度为n的数列ai,求ai的子序列bi的最长长度,满足bi&bi-1!=0。n≤100000,ai≤10^9。
用f[i]表示当前二进制i为1的最长子序列长度。每次求所有((1<<i)&bi)==1的f[i]最大值max,将所有((1<<i)&bi)==1的f[i]变为max+1。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a,f[40],tot;
int main(){
n=read();
inc(i,1,n){
a=read(); tot=0;
inc(j,0,30)if(a&(1<<j))tot=max(tot,f[j]); inc(j,0,30)if(a&(1<<j))f[j]=tot+1;
}
tot=0; inc(i,0,30)tot=max(tot,f[i]); printf("%d",tot); return 0;
}n头牛,如果某头牛左边距离D以内有高度至少是它的两倍的牛,右边也有,则此牛会感觉到不舒服。问多少牛会不舒服。n≤50000
用单调队列维护距离D以内的区间最大值,判断是否至少是当前牛的两倍,再倒回去做一遍即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct nd{int x,h;}; nd nds[maxn];
bool cmp(nd a,nd b){return a.x<b.x;}
int n,d,q1[maxn],q2[maxn],l,r,ans; bool unc[maxn];
int main(){
n=read(); d=read(); inc(i,1,n)nds[i].x=read(),nds[i].h=read(); sort(nds+1,nds+n+1,cmp); r=0; l=1;
inc(i,1,n){
while(l<=r&&nds[i].x-q1[l]>d)l++; if(l<=r&&q2[l]>=(nds[i].h<<1))unc[i]=1;
while(l<=r&&q2[r]<nds[i].h)r--; q1[++r]=nds[i].x; q2[r]=nds[i].h;
}
r=0; l=1;
for(int i=n;i>=1;i--){
while(l<=r&&q1[l]-nds[i].x>d)l++; if(l<=r&&q2[l]>=(nds[i].h<<1)&&unc[i])ans++;
while(l<=r&&q2[r]<nds[i].h)r--; q1[++r]=nds[i].x; q2[r]=nds[i].h;
}
printf("%d",ans); return 0;
}n*n的网格中有k头牛。在一个格子里发射子弹可以射中本格子,同行,同列,左斜线,右斜线(就是一个米字形)的牛,问能射中所有牛的格子有几个。n≤100。
枚举所有格子,从当前格子出发按题目里的方向走累计被射中的牛即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 110
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn][maxn],n,k,ans;
int main(){
n=read(); k=read(); inc(i,1,k){int x=read(),y=read(); a[x][y]++;}
inc(i,1,n)inc(j,1,n){
int tot=0; inc(l,1,n)tot+=a[i][l]+a[l][j];
int kx=i,ky=j; while(kx>=1&&ky>=1)tot+=a[kx][ky],kx--,ky--;
kx=i; ky=j; while(kx<=n&&ky<=n)tot+=a[kx][ky],kx++,ky++;
kx=i; ky=j; while(kx>=1&&ky<=n)tot+=a[kx][ky],kx--,ky++;
kx=i; ky=j; while(kx<=n&&ky>=1)tot+=a[kx][ky],kx++,ky--;
tot-=5*a[i][j]; if(tot==k)ans++;
}
printf("%d",ans); return 0;
}给一个数n,对其进行k次变换,第i次变换是将当前的n变成大于等于n的最小的i的倍数。求k次变换后n为多少。n≤10^10,k≤10^10。
对n的变换可以表示成ceil(n/i)*i。有一个结论,当i第一次大于sqrt(当前的n)后,以后的i将永远大于sqrt(那时的n),且从这以后ceil(n/i)都相等。因此可以先暴力变换n,当i大于sqrt(当前n)后,求出ceil(n/i),直接乘k就是最后答案。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define ll long long
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
ll n,k; int t;
int main(){
while(1){
n=read(); k=read(); if(n==0&&k==0)break; t++; int i;
for(i=1;i<=k&&i<=(int)sqrt(n)+1;i++)n=(n+i-1)/i*i;
if(i==k+1)printf("Case #%d: %lld\n",t,n);
else{n/=(i-1); printf("Case #%d: %lld\n",t,n*k);}
}
return 0;
}输入R,M,Y,求出(1+R%)^Y*M。R≤20,Y≤400
恐怕是bzoj最水的题了……
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
int main(){
double n,m; int y; scanf("%lf%lf%d",&n,&m,&y); n=n/100+1; inc(i,1,y)m*=n; printf("%d",int(m)); return 0;
}给定n个数,请从中选出若干个数,使得总和为偶数,请最大化这个总和。n≤1000000。
如果这n个数中有偶数个奇数,就将所有数都选出;否则放弃最小的奇数,选出剩下的数。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1000010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn],tot,sm,mn,n;
int main(){
n=read(); inc(i,1,n)a[i]=read(),sm+=a[i]; if(n==1&&(a[1]&1))puts("NIESTETY");else{
inc(i,1,n)if(a[i]&1)tot++; if(!(tot&1))printf("%d",sm);else{
mn=0x3fffffff; inc(i,1,n)if(a[i]&1&&mn>a[i])mn=a[i]; printf("%d",sm-mn);
}
}
return 0;
}一个长度为n的序列,每个元素有一定概率是1,不是1就是0。连续x个1可以贡献x^3的分数,问期望分数。
期望dp。f1[i]表示连续到i的期望长度,f2[i]表示期望的f1[i]^2,f3[i]表示期望的f1[i]^3。
f1[i]=(f1[i-1]+1)*p,f2[i]=(f2[i-1]+2*f1[i-1]+1)*p,f3[i]=f3[i-1]+3*f2[i-1]+3*f1[i-1]+1。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
double f1[maxn],f2[maxn],f3[maxn]; int n;
int main(){
scanf("%d",&n);
inc(i,1,n){
double a; scanf("%lf",&a);
f1[i]=(f1[i-1]+1)*a; f2[i]=(f2[i-1]+2*f1[i-1]+1)*a;
f3[i]=f3[i-1]+(f1[i-1]*3+f2[i-1]*3+1)*a;
}
printf("%.1lf",f3[n]); return 0;
}N个单位时间,每个单位时间可以进行一项特技动作,可选的动作有K种,每种动作有一个刺激程度Ci。每次动作的价值为(距上次该动作的时间)*Ci,若为第一次进行该动作,价值为0。求最大总价值。N≤1000,K≤300。
因为如果同个动作做3次,不如只做头尾两次更好。所以把动作按Ci降序排序,把Ci大的尽量放在两端。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,k,a[maxn],ans;
int main(){
n=read(); k=read(); inc(i,1,k)a[i]=read(); sort(a+1,a+k+1); int l=1,r=n;
for(int i=k;i>=1;i--){
ans+=(r-l)*a[i]; r--; l++; if(l>=r)break;
}
printf("%d",ans); return 0;
}给一个序列,将其修改为不下降序列,要求修改幅度最大的幅度尽量小。序列大小≤5000000
最优策略是将其全部修改为同个值,且这个值是序列中两个相差最大的元素的差值/2。故输出这个值即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 5000010
#define ll long long
using namespace std;
int n; ll sa,sb,sc,sd,a[maxn],mod,mx[maxn],ans;
ll f(ll a){return (a*a%mod*a%mod*sa%mod+a*a%mod*sb%mod+a*sc%mod+sd)%mod;}
int main(){
scanf("%d%lld%lld%lld%lld%lld%lld",&n,&sa,&sb,&sc,&sd,&a[1],&mod);
inc(i,2,n)a[i]=(f(a[i-1])+f(a[i-2]))%mod; inc(i,1,n)mx[i]=max(mx[i-1],a[i]);
inc(i,1,n)if(mx[i-1]>a[i])ans=max(ans,(mx[i-1]-a[i]+1)>>1); printf("%lld",ans); return 0;
}维护数据结构,支持区间第k大和单点修改。序列大小,操作数≤10000
构造一个树状数组,树状数组中的节点用主席树维护。一开始先插入序列中的节点,然后对于修改,就是将经过的树状数组上的主席树删除旧值,再插入新值;对于查询,还是和普通主席树一样二分,但此时的前缀和是由树状数组中数棵主席树查询节点的和得到的。反思:空间复杂度粗略计算是O(nlog^2n),常数大概是乘个7,8,在bzoj上内存达到了80M,幸好bzoj上空间给的是128M,听说原题空间是31M,规模是30000,我要是做原题早挂了!不知道怎么办QAQ
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 10010
#define lb(x) x&-x
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,a[maxn],v[maxn*2],tot,root[maxn],sz[3*maxn*15*15],ch[3*maxn*15*15][2],cnt;
struct ask{char opt[3]; int l,r,k;}; ask asks[maxn];
struct ls{int id,v;}; ls lss[maxn*2]; int lsss;
bool cmp(ls a,ls b){return a.v<b.v;}
void lisan(){
inc(i,1,n)lss[++lsss]=(ls){i,a[i]};
inc(i,1,m)if(asks[i].opt[0]=='C')lss[++lsss]=(ls){n+i,asks[i].k};
sort(lss+1,lss+1+lsss,cmp);
inc(i,1,lsss){
if(i==1||lss[i].v!=lss[i-1].v)tot++,v[tot]=lss[i].v;
if(lss[i].id<=n)a[lss[i].id]=tot;else asks[lss[i].id-n].k=tot;
}
}
int build(int l,int r){
int x=++cnt; sz[x]=0; if(l==r)return x;
int mid=(l+r)>>1; ch[x][0]=build(l,mid); ch[x][1]=build(mid+1,r); return x;
}
void updseg(int &x,int y,int l,int r,int a){
cnt++; ch[cnt][0]=ch[x][0]; ch[cnt][1]=ch[x][1]; sz[cnt]=sz[x]+a; x=cnt; if(l==r)return;
int mid=(l+r)>>1; if(y<=mid)updseg(ch[x][0],y,l,mid,a); if(y>mid)updseg(ch[x][1],y,mid+1,r,a);
}
int queryseg(int x,int ql,int qr,int l,int r){
if(ql<=l&&r<=qr)return sz[x]; int mid=(l+r)>>1,q=0;
if(ql<=mid)q+=queryseg(ch[x][0],ql,qr,l,mid); if(mid<qr)q+=queryseg(ch[x][1],ql,qr,mid+1,r);
return q;
}
void updbit(int x,int y,int a){
while(x<=n)updseg(root[x],y,1,tot,a),x+=lb(x);
}
int querybit(int x,int ql,int qr){
int q=0; while(x>=1)q+=queryseg(root[x],ql,qr,1,tot),x-=lb(x); return q;
}
void init(){
int x=build(1,tot); inc(i,1,n)root[i]=x; inc(i,1,n)updbit(i,a[i],1);
}
int query(int ql,int qr,int k){
int l=1,r=tot;
while(1){
int mid=(l+r)>>1; int x=querybit(qr,l,mid)-querybit(ql-1,l,mid);
if(x>=k)r=mid;else l=mid+1,k-=x; if(l==r)return l;
}
}
void modify(int x,int y){
updbit(x,a[x],-1); updbit(x,y,1); a[x]=y;
}
int main(){
n=read(); m=read(); inc(i,1,n)a[i]=read();
inc(i,1,m){
scanf("%s",asks[i].opt);
if(asks[i].opt[0]=='Q')asks[i].l=read(),asks[i].r=read(),asks[i].k=read();
if(asks[i].opt[0]=='C')asks[i].l=read(),asks[i].k=read();
}
lisan(); init();
inc(i,1,m){
if(asks[i].opt[0]=='Q')printf("%d\n",v[query(asks[i].l,asks[i].r,asks[i].k)]);
if(asks[i].opt[0]=='C')modify(asks[i].l,asks[i].k);
}
return 0;
}判断给定的数字能否被表示成两个斐波那契数的乘积。n≤10^9
开始在想有没有什么根号级算法,后来想知道斐波那契数列10000位有多大,结果爆long long了……实际上斐波那契数列到45位就大于10^9了。所以直接枚举即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 45
using namespace std;
int a[maxn+5]; int t;
int main(){
a[1]=1; a[2]=1; inc(i,3,maxn)a[i]=a[i-1]+a[i-2]; scanf("%d",&t);
while(t--){
int b; scanf("%d",&b); if(b==0){puts("TAK"); continue;} bool f=0;
inc(i,1,maxn){
inc(j,1,maxn)if((long long)a[i]*a[j]==b){puts("TAK"); f=1; break;}
if(f)break;
}
if(!f)puts("NIE");
}
return 0;
}找一个01串中出现次数大于1的字串。01串长度≤3000
有个结论:一个串的所有后缀的所有前缀对应了这个串的字串。所以将这个串的所有后缀插入trie,累计经过trie上每个节点的经过次数,找到大于1的输出即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 3010
using namespace std;
int n,ch[maxn*maxn][2],sm[maxn*maxn],tot; char s[maxn];
void insert(int x){
int y=0;
inc(j,x,n){
if(!ch[y][s[j]-'0'])tot++,ch[y][s[j]-'0']=tot,y=tot;else y=ch[y][s[j]-'0']; sm[y]++;
}
}
void print(int x){
if(sm[x]>1)printf("%d\n",sm[x]);
if(ch[x][0])print(ch[x][0]); if(ch[x][1])print(ch[x][1]);
}
int main(){
scanf("%d",&n); scanf("%s",s+1); inc(i,1,n)insert(i);
if(ch[0][0])print(ch[0][0]); if(ch[0][1])print(ch[0][1]); return 0;
}给你一个N*N的矩阵,每行有一个障碍,数据保证任意两个障碍不在同一行,任意两个障碍不在同一列。要求你放N枚棋子(障碍的位置不能放棋子),也满足每行只有一枚棋子,每列只有一枚棋子的限制,求有多少种方案。N≤200。
发现在障碍在什么位置和答案无关。因此可以把棋子摆成左上-右下对角线,然后就是错排问题(一个长度为n的排列,要求每个元素不能放在与自己编号相同的位置上,问有多少种方案满足条件)了。错排公式:f[i]=(f[i-1]+f[i-2])*(i-1),特别的,f[0]=1,f[1]=0。本弱太懒了,不想写高精度,写了个python,结果因为不会写wa了好几发QAQ
//python的高亮好丑啊!
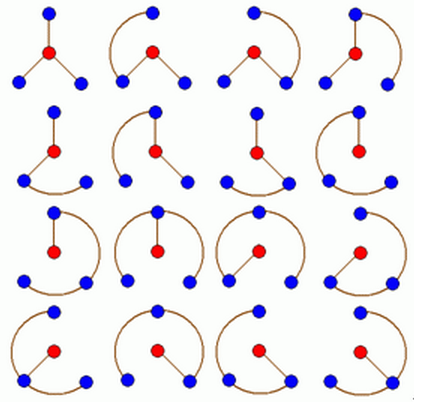
N轮状病毒的产生规律是在一个N轮状基中删去若干条边,使得各原子之间有唯一的信息通道,例如共有16个不 同的3轮状病毒,如下图所示

现给定n,计算有多少个不同的n轮状病毒。N<=100
公式:f[i]=f[i-1]*3-f[i-2]+2,i≥3,f[1]=1,f[2]=5。(我承认我是抄的QAQ因为我根本不懂什么矩阵树定理~
又是高精度,又被我用python水掉了……
给一个只由JOI三个字母组成的串,求最长的一个子串使其中JOI三个字母出现次数相等。串长度≤200000
有点像bzoj4384,因此推算的过程是差不多的,但还是有不同因为本题要求的是出现次数相等,而那题要求的是不等:
cnt[1][i]-cnt[1][j]==cnt[2][i]-cnt[2][j],cnt[2][i]-cnt[2][j]==cnt[3][i]-cnt[3][j],cnt[1][i]-cnt[1][j]==cnt[3][i]-cnt[3][j]
化简得到cnt[1][i]-cnt[2][i]==cnt[1][j]-cnt[2][j],cnt[2][i]-cnt[3][i]==cnt[2][j]-cnt[3][j],cnt[1][i]-cnt[3][i]==cnt[1][j]-cnt[3][j](本式实际上是冗余的因为可由前两式相加得到)
故可以用一个map维护二元组<cnt[1][i]-cnt[2][i],cnt[2][i]-cnt[3][i]>的最早出现次数i,每次在map中查找键值中有没有和当前元素的<cnt[1]-cnt[2],cnt[2]-cnt[3]>相等的元素,有的话和答案比较,否则插入map。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
#define maxn 200100
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
int a,b,c,d,e,n,ans; char s[maxn];
map<pair<int,int>,int>m;
int main(){
scanf("%d%s",&n,s+1); m[make_pair(0,0)]=0;
inc(i,1,n){
if(s[i]=='J')a++; if(s[i]=='O')b++; if(s[i]=='I')c++; d=a-b; e=b-c;
if(m.find(make_pair(d,e))==m.end())m[make_pair(d,e)]=i;
else ans=max(ans,i-m[make_pair(d,e)]);
}
printf("%d",ans); return 0;
}求有多少种长度为n的序列 A,满足1~n在序列中各出现了一次,且序列恰好有m个数是稳定的(若第i个数A[i]的值为i,则称i是稳定的)。共T组数据,方案数模10^9+7。T=500000,n≤1000000,m≤1000000。
显然结果为C(n,m)*f[n-m],f[n-m]为错排数满足f[i]=(f[i-1]+f[i-2])*(i-1),f[1]=0,f[0]=1。因为n,m过大,求组合数的递推法行不通,因此只能用公式:C(n,m)=n!/(m!*(n-m)!),n!先递推出来,因为最后有除法,故还须求个逆元,刚好模数是质数,所以利用费马小定理,写个快速幂就好了。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1000010
#define mod 1000000007
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
long long power(int a,int b){
if(b==0)return 1; if(b==1)return a;
long long c=power(a,b>>1);
if(b&1)return c*c%mod*a%mod;else return c*c%mod;
}
long long a[maxn],b[maxn]; int t,n,m;
long long c(int n,int m){
return a[n]*power(a[n-m]*a[m]%mod,mod-2)%mod;
}
int main(){
a[0]=1; inc(i,1,maxn-10)a[i]=a[i-1]*i%mod; b[0]=1; b[1]=0; inc(i,2,maxn-10)b[i]=(b[i-1]+b[i-2])%mod*(i-1)%mod;
t=read();
while(t--){n=read(); m=read(); printf("%lld\n",c(n,m)*b[n-m]%mod);}
return 0;
}N柱砖,希望有连续K柱的高度是一样的. 你可以选择以下两个动作 1:丢掉某柱砖的一块砖。给某柱加上一块砖,现在希望用最小次数的动作完成任务。N≤100000
设一个区间长度为k,其中位数为a,比a小的元素个数为b,和为c;比a大的元素个数为d,和为e。则题目要求维护一个长度为k的滑动窗口,能求出它的b*a-c+e-d*a。故用一个维护sum,size两个值的treap来维护。然而似乎我想复杂了?比所有人代码都大1k!注意要开long long。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cstdlib>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
#define ll long long
#define qs(x,y) qs(x,y)
#define qb(x,y) qb(x,y)
#define qss(x,y) qss(x,y)
#define qbs(x,y) qbs(x,y)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int ch[maxn][2],sz[maxn],cnt[maxn],rnd[maxn],n,k,tot,root; ll a[maxn],sm[maxn],v[maxn],ans;
void update(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x],sm[x]=sm[ch[x][0]]+sm[ch[x][1]]+v[x]*cnt[x];}
void rotate(int &x,bool a){int y=ch[x][a]; ch[x][a]=ch[y][!a]; ch[y][!a]=x; update(x); update(y); x=y;}
void ins(int &x,ll val){
if(!x){x=++tot; v[x]=sm[x]=val; rnd[x]=rand(); ch[x][0]=ch[x][1]=0; sz[x]=cnt[x]=1; return;}
if(v[x]==val){cnt[x]++; sz[x]++; sm[x]+=val; return;}
if(val<v[x]){ins(ch[x][0],val); update(x); if(rnd[ch[x][0]]<rnd[x])rotate(x,0); return;}
if(val>v[x]){ins(ch[x][1],val); update(x); if(rnd[ch[x][1]]<rnd[x])rotate(x,1); return;}
}
void del(int &x,ll val){
if(v[x]==val){
if(cnt[x]>1){cnt[x]--; sz[x]--; sm[x]-=val; return;}
else{
if(!ch[x][0]||!ch[x][1])x=ch[x][0]+ch[x][1];
else{
if(rnd[ch[x][0]]<rnd[ch[x][1]])rotate(x,0),del(ch[x][1],val),update(x);
else rotate(x,1),del(ch[x][0],val),update(x);
}
return;
}
}
if(val<v[x]){del(ch[x][0],val); update(x); return;}
if(val>v[x]){del(ch[x][1],val); update(x); return;}
}
int find(int x,int k){
if(k>sz[ch[x][0]]&&k<=sz[ch[x][0]]+cnt[x])return x;
if(k<=sz[ch[x][0]])return find(ch[x][0],k);
if(k>sz[ch[x][0]]+cnt[x])return find(ch[x][1],k-sz[ch[x][0]]-cnt[x]);
}
ll qs(int x,ll val){
if(val<v[x])return qs(ch[x][0],val);
if(val==v[x])return sm[ch[x][0]];
if(val>v[x])return sm[x]-sm[ch[x][1]]+qs(ch[x][1],val);
}
ll qb(int x,ll val){
if(val>v[x])return qb(ch[x][1],val);
if(val==v[x])return sm[ch[x][1]];
if(val<v[x])return sm[x]-sm[ch[x][0]]+qb(ch[x][0],val);
}
int qss(int x,ll val){
if(val<v[x])return qss(ch[x][0],val);
if(val==v[x])return sz[ch[x][0]];
if(val>v[x])return sz[x]-sz[ch[x][1]]+qss(ch[x][1],val);
}
int qbs(int x,ll val){
if(val>v[x])return qbs(ch[x][1],val);
if(val==v[x])return sz[ch[x][1]];
if(val<v[x])return sz[x]-sz[ch[x][0]]+qbs(ch[x][0],val);
}
int main(){
n=read(); k=read(); inc(i,1,n)a[i]=read(); inc(i,1,k)ins(root,a[i]); int l=1,r=k;
ans=1LL*100000000000;
while(1){
ll x=v[find(root,(k>>1)+1)];
ans=min(ans,x*qss(root,x)-qs(root,x)+qb(root,x)-qbs(root,x)*x);
del(root,a[l]); l++; r++; if(r>n)break; ins(root,a[r]);
}
printf("%lld",ans); return 0;
}给你一个序列,你最多可以删去k类数(数列中相同的数字被称为一类数)。求通过删数得到的该序列中的最长完美序列(满足所有的数字相等的连续子序列被叫做完美序列)。序列大小≤100000
先离散化,然后维护一个单调队列,如果当前类数小于等于k+1就比较答案,否则左端点++。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct ls{int id,v;}; ls lss[maxn]; int tot,v[maxn],n,k,l,r,cnt[maxn],mx,kinds;
bool cmp(ls a,ls b){return a.v<b.v;}
int main(){
n=read(); k=read(); inc(i,1,n)lss[i]=(ls){i,read()}; sort(lss+1,lss+n+1,cmp);
inc(i,1,n){if(i==1||lss[i].v!=lss[i-1].v)tot++; v[lss[i].id]=tot;}
l=1; r=1; kinds=0;
while(1){
while(r<=n&&kinds<=k+1){
cnt[v[r]]++; if(cnt[v[r]]==1)kinds++; mx=max(mx,cnt[v[r]]); r++;
}
if(r==n+1)break;
while(kinds>k+1){
cnt[v[l]]--; if(!cnt[v[l]])kinds--; l++;
}
}
printf("%d",mx); return 0;
}n头牛,d种疾病,每头牛都患一些疾病,现在要求选出最多的牛,使这些牛患病的种类数不超过k。n≤1000,d≤15
状压dp。f[i][S]表示当前考虑i头牛,患病集合为S,
则f[i][S]=max(f[i+1][S|si]+1,f[i+1][S]),S|si为1的位不超过k且S为1的位不超过k
=f[i+1][S],S|si为1的位超过k且S为1的位不超过k
可以先对每个状态预处理以下判断它为1的位数是否超过了k。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 40000
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int f[2][maxn],n,d,k,a[maxn/20],x,y; bool no[maxn];
void init(){
inc(i,0,(1<<d)-1){
no[i]=0; int tot=0;
for(int j=0;(1<<j)<=i;j++)if(i&(1<<j)){
tot++; if(tot>k){no[i]=1; break;}
}
}
}
int main(){
n=read(); d=read(); k=read(); init();
inc(i,1,n){int x=read(); inc(j,1,x){int y=read(); a[i]|=(1<<(y-1));}}
x=0; y=1;
for(int i=n;i>=1;i--){
inc(j,0,(1<<d)-1)if(!no[j]){
int z=j|a[i]; if(no[z])f[y][j]=f[x][j];else f[y][j]=max(f[x][z]+1,f[x][j]);
}
swap(x,y);
}
printf("%d",f[x][0]); return 0;
}给一个字符串,求最长的k个回文子串(此处回文子串长度必须为奇数)长度的乘积。字符串长度≤1000000
先用manacher预处理出第i个字符为中心的最长回文子串一端长度p[i],然后cnt[1]++,cnt[2*p[i]+1]–,最后cnt[i]+=cnt[i-2]求出所有长度的回文子串个数。然后用快速幂求出相同长度的回文子串的长度乘积即可。注意k要开long long!
反思:manacher是一种用来O(n)求每个字符为中心的最长回文子串一端长度的算法(如果要求的回文子串长度可以是偶数,就在原串两端和每两个字符之间插入一个特殊字符,最后答案/2即可)。主要思想是当前求的p[i]和它的某个对称点j是等价的,可以借助p[j]来求。具体看这个。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1000010
#define mod 19930726
#define ll long long
using namespace std;
int n,mx,id,p[maxn],cnt[maxn]; char s[maxn]; ll ans,k;
ll power(ll a,int b){
if(b==0)return 1; if(b==1)return a;
ll c=power(a,b>>1);
if(b&1)return c*c%mod*a%mod;else return c*c%mod;
}
int main(){
scanf("%d%lld",&n,&k); scanf("%s",s+1); mx=0; id=0;
inc(i,1,n){
if(mx>i)p[i]=min(p[2*id-i],mx-i);else p[i]=1;
while(i-p[i]>=1&&i+p[i]<=n&&s[i-p[i]]==s[i+p[i]])p[i]++; cnt[1]++; cnt[2*p[i]+1]--;
if(mx<i+p[i]-1)mx=i+p[i]-1,id=i;
}
inc(i,3,n)if(i&1)cnt[i]+=cnt[i-2]; ans=1;
for(int i=n;i>=1;i--){
if(cnt[i]){
if(k>=cnt[i]){ans=(ans*power(i,cnt[i]))%mod; k-=cnt[i];}else{ans=(ans*power(i,k))%mod; k=0;}
if(!k)break;
}
}
if(k)printf("-1");else printf("%lld",ans); return 0;
}丢番图方程:1/x+1/y=1/n(x,y,n∈N+) ,给定n,求出关于n的丢番图方程有多少组解。n≤10^14。
通分得yn+xn=xy,即xy-xn-yn+n^2=n^2,即(x-n)(y-n)=n^2,故x-n是n^2的因数,所有答案为n^2的因数个数/2,向上取整。一个数的因数个数为该数每种质因数的个数+1的乘积。所以先将n分解质因数,然后ans乘上个数*2+1(因为要求n^2的因数个数)。如果最后n>1,说明有一个质因数大于sqrt(n),则ans还要乘3。最后输出(ans+1)/2即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
using namespace std;
long long n,ans;
int main(){
scanf("%lld",&n); ans=1;
for(int i=2;(ll)i*i<=n;i++)if(n%i==0){
int j=0; while(n%i==0)n/=i,j++; ans*=(j<<1|1); if(n==1)break;
}
if(n>1)ans*=3;
printf("%lld",(ans+1)>>1); return 0;
}求在一个序列中和在区间[l,r]中的连续子序列的个数。序列大小≤100000,序列元素可以为负数。
题目要求这个:l<=sum[i]-sum[j-1]<=r,移项得sum[i]-l>=sum[j-1]>=sum[i]-r,故题目转化为求一个集合中值在某个区间的元素个数。神犇们的题解里用的都是权值线段树,然而我不知道怎么离散化,所以写了一个treap,不过由于写得不熟,又WA了好几发。注意检查有没有需要用long long的地方却没用。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <set>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define ll long long
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
ll v[maxn]; int ch[maxn][2],sz[maxn],cnt[maxn],tot,root,rnd[maxn];
void update(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];}
void rotate(int &x,bool c){
int y=ch[x][c]; ch[x][c]=ch[y][!c]; ch[y][!c]=x; update(x); update(y); x=y;
}
void insert(int &x,ll val){
if(!x){x=++tot; sz[x]=cnt[x]=1; v[x]=val; rnd[x]=rand(); return;}
if(val==v[x]){cnt[x]++; sz[x]++; return;}
if(val<v[x]){insert(ch[x][0],val); update(x); if(rnd[ch[x][0]]<rnd[x])rotate(x,0); return;}
if(val>v[x]){insert(ch[x][1],val); update(x); if(rnd[ch[x][1]]<rnd[x])rotate(x,1); return;}
}
int query1(int x,ll val){
if(!x)return 0;
if(val<v[x])return sz[ch[x][1]]+cnt[x]+query1(ch[x][0],val);
if(val==v[x])return sz[ch[x][1]]+cnt[x];
if(val>v[x])return query1(ch[x][1],val);
}
int query2(int x,ll val){
if(!x)return 0;
if(val<v[x])return sz[ch[x][1]]+cnt[x]+query2(ch[x][0],val);
if(val==v[x])return sz[ch[x][1]];
if(val>v[x])return query2(ch[x][1],val);
}
int n; ll sm,ans,l,r;
int main(){
n=read(); l=read(); r=read(); insert(root,0);
inc(i,1,n){
ll a=read(); sm+=a; int x=query1(root,sm-r),y=query2(root,sm-l); ans+=(ll)x-y; insert(root,sm);
}
printf("%lld",ans); return 0;
}判定有多少对字符串只有一个字母不同。字符串个数≤30000,长度≤300。
求出第i个字符串前j个字符的哈希值hs[i][j],然后枚举去掉所有字符串的第几位,将去掉后的字符串的哈希值用hs数组直接算出,排序后检查有没有相同的计入答案。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 30010
#define hash 2333
#define ll unsigned long long
using namespace std;
ll hs[maxn][210],tmp[maxn],power[maxn],ans; int n,k,s; char str[210];
int main(){
scanf("%d%d%d",&n,&k,&s); power[0]=1; inc(i,1,k)power[i]=power[i-1]*hash;
inc(i,1,n){
scanf("%s",str+1); inc(j,1,k)hs[i][j]=hs[i][j-1]*hash+str[j];
}
inc(i,1,k){
inc(j,1,n)tmp[j]=hs[j][k]-hs[j][i]*power[k-i]+hs[j][i-1]*power[k-i+1];
sort(tmp+1,tmp+1+n); int cnt=1;
inc(j,2,n)if(tmp[j]==tmp[j-1])ans+=cnt,cnt++;else cnt=1;
}
printf("%llu",ans); return 0;
}给出一个序列,你能将一个长度不超过d的连续子序列全部变为0,要求和不超过p的最长连续子序列。序列大小≤2000000。
用两个指针,每次右指针右移时就将新加入元素所能消掉的区间加入单调队列,如果当前区间和减单调队列中最大的元素不超过p,则累计答案,否则左指针左移并在单调队列中删掉这个元素(如果存在的话)。反思:本弱wa了4发,对拍查不出错误,后来和标程一点一点对比,才发现问题。原因是ans没有初始化为d(见我的烂代码),这样的话如果遇到这个数据就会挂:
2 0 1
1 2
结果会输出0。不过根本原因是我程序写得不好,容易出bug。
我的烂代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 2000010
#define ll long long
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
ll a[maxn],sum[maxn],q1[maxn],now,p; int q2[maxn],l,r,ql,qr,ans,n,d;
int main(){
n=read(); p=read(); d=read();
if(d>=n){printf("%d",n); return 0;}
inc(i,1,n)a[i]=read(),sum[i]=sum[i-1]+a[i];
l=1; r=d; ql=qr=1; q1[1]=now=sum[r]-sum[l-1]; q2[1]=1; ans=d;
while(1){
while(r<n&&(r-l+1<d||now<=p+q1[ql])){
r++; now+=a[r];
while(ql<=qr&&sum[r]-sum[r-d]>=q1[qr])qr--;
q1[++qr]=sum[r]-sum[r-d]; q2[qr]=r-d+1;
if(now<=p+q1[ql])ans=max(ans,r-l+1);
}
if(r==n)break; now-=a[l]; if(ql<=qr&&q2[ql]<=l)ql++; l++;
}
printf("%d",ans); return 0;
}照标程写的代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 2000010
#define ll long long
using namespace std;
inline ll read(){
char ch=getchar(); ll f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
ll a[maxn],sum[maxn],q1[maxn],now,p; int q2[maxn],l,r,ql,qr,ans,n,d;
int main(){
n=read(); p=read(); d=read();
if(d>=n){printf("%d",n); return 0;}
inc(i,1,n)a[i]=read(),sum[i]=sum[i-1]+a[i];
l=1; r=d; ql=qr=1; q1[1]=now=sum[r]-sum[l-1]; q2[1]=1;
while(r<n){
r++; now+=a[r]; while(ql<=qr&&sum[r]-sum[r-d]>=q1[qr])qr--;
q1[++qr]=sum[r]-sum[r-d]; q2[qr]=r-d+1;
while(now>p+q1[ql]){now-=a[l]; if(q2[ql]<=l)ql++; l++;}
ans=max(ans,r-l+1);
}
printf("%d",ans); return 0;
}无向图,从源点出发,去两个地方,问最短路径是多少。两个地方去的先后没有要求,且从一个地方到另一个地方不用经过源点。点数≤100000。
求源点对所有点的最短路和一个地方到所有点的最短路,比较一下即可。听说本题需要用队列优化的spfa或dijkstra才能过,本弱写了dijkstra(反正STL优先队列不要钱)。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int t,w,n;}; e es[maxn*4]; int g[maxn],ess;
void pe(int f,int t,int w){
es[++ess]=(e){t,w,g[f]}; g[f]=ess;
es[++ess]=(e){f,w,g[t]}; g[t]=ess;
}
struct nd{
int d,u;
bool operator < (const nd &a)const{return d>a.d;}
};
priority_queue <nd> q; int d[maxn]; bool vis[maxn];
void dijkstra(int s){
while(!q.empty())q.pop(); memset(d,-1,sizeof(d));
memset(vis,0,sizeof(vis)); d[s]=0; q.push((nd){0,s});
while(1){
int x=q.top().u; while(!q.empty()&&vis[x])q.pop(),x=q.top().u;
if(q.empty()&&vis[x])break; vis[x]=1;
for(int i=g[x];i;i=es[i].n)
if(d[es[i].t]==-1||d[es[i].t]>d[x]+es[i].w){
d[es[i].t]=d[x]+es[i].w;
q.push((nd){d[es[i].t],es[i].t});
}
}
}
int p,c,pb,pa1,pa2,dis1,dis2,dis3;
int main(){
c=read(); p=read(); pb=read(); pa1=read(); pa2=read();
inc(i,1,c){int a=read(),b=read(),c=read(); pe(a,b,c);}
dijkstra(pb); dis1=d[pa1]; dis2=d[pa2]; dijkstra(pa1); dis3=d[pa2];
if(dis1<dis2)printf("%d",dis1+dis3);else printf("%d",dis2+dis3);
return 0;
}m个要求,每个要求由一个长度为n的01串和一个数组成,表示只有与给出的01串按位与后1的个数为给出数的01串满足要求。求满足所有要求的01串。m≤100,n≤20。
暴力枚举01串,我以为会超时,但没有。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 30
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn*10][maxn]; int n,m,b[maxn*10],ans;
bool check(int x){
inc(i,1,m){
int k=0; inc(j,0,n-1)if(x&(a[i][j+1]<<j))k++;
if(k!=b[i])return 0;
}
return 1;
}
int main(){
n=read(); m=read();
inc(i,1,m){
char ch=getchar(); while(ch<'0'||ch>'9')ch=getchar(); int j=0;
while(ch>='0'&&ch<='9')a[i][++j]=ch-'0',ch=getchar();
b[i]=read();
}
ans=-1;
inc(i,0,(1<<n)-1){
if(check(i)){
if(ans!=-1){printf("NOT UNIQUE"); return 0;}else ans=i;
}
}
if(ans==-1)printf("IMPOSSIBLE");else{
inc(i,0,n-1)printf("%d",ans&(1<<i)?1:0);
}
return 0;
}给个字符串集,询问字符串集中以字符串s为前缀的第k小字符串编号多少。字符串集总长度≤3000000,询问数≤1000,询问字符串长度≤1000。
先吐槽一下bzoj:自己加强了数据也不说一声,明明字符串集总长度不只1000000,不过我也不知道是不是3000000,反正2000000会RE。
一看到字符串集,以为是trie,结果又MLE又TLE,改左兄弟右儿子表示法又写炸。看题解trie求DFS序然后用主席树维护……天啊怎么银组题也这么劲QAQ。后来受神犇ccz教,原来只要先给字符串集排序,然后二分找区间就行了,usaco题解也是这样写的。写完了结果re无数次,本机测usaco数据什么事也没有,最后一怒之下数组开到3000000,过了~注意因为只给出字符串集总长度不知道字符串个数,所以字符串要用一个链表维护。(然而正常人都是用STLstring不会RE不说代码还比我少一半,我太弱了QAQ)
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 3000010
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct hd{int nx,id;}; hd hds[maxn];
struct nd{char ch; int nx;}; nd nds[maxn]; int ndss;
bool cmp(hd a,hd b){
int j=a.nx,k=b.nx;
while(j&&k){
if(nds[j].ch<nds[k].ch)return 1;
if(nds[j].ch>nds[k].ch)return 0;
j=nds[j].nx; k=nds[k].nx;
}
if(!j&&!k)return a.id<b.id;
if(!j)return 1;else return 0;
}
int w,n; char str[maxn];
int check(int x){
x=hds[x].nx; int len=strlen(str+1);
for(int i=1;i<=len;i++,x=nds[x].nx){
if(!x||str[i]>nds[x].ch)return 1;
if(str[i]<nds[x].ch)return -1;
}
return 0;
}
int main(){
w=read(); n=read();
inc(i,1,w){
char ch=getchar(); while(ch<'a'||ch>'z')ch=getchar();
hds[i]=(hd){++ndss,i};
while(ch>='a'&&ch<='z')
nds[ndss]=(nd){ch,ndss+1},ndss++,ch=getchar();
nds[--ndss].nx=0;
}
sort(hds+1,hds+1+w,cmp);
inc(i,1,n){
int k=read(); scanf("%s",str+1);
int q=-1,l=1,r=w;
while(l<=r){
int mid=(l+r)>>1; int c=check(mid);
if(c==0)q=mid,r=mid-1;
else if(c==-1)r=mid-1;else l=mid+1;
}
if(q==-1||q+k-1>w||check(q+k-1)!=0)printf("-1\n");
else printf("%d\n",hds[q+k-1].id);
}
return 0;
}n头牛进行锦标赛,每场比赛的好看程度是两头牛的编号异或和,并总有一方被淘汰。求安排比赛(可以决定比赛胜负)可以得到的最大总好看程度是多少。n≤2000
先求出牛两两之间的异或和,然后发现可以把比赛看做连边,且共有n-1场比赛,所以求最大生成树就行了。神犇们用的都是Prim,蒟蒻不会,用Kruscal结果时间排倒数。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 2010
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn],fa[maxn],n,cnt; long long ans;
struct e{int f,t,w;}; e es[maxn*maxn]; int ess;
bool cmp(e a,e b){return a.w>b.w;}
int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
int main(){
n=read(); inc(i,1,n)a[i]=read(),fa[i]=i;
inc(i,1,n)inc(j,i+1,n)es[++ess]=(e){i,j,a[i]^a[j]};
sort(es+1,es+1+ess,cmp);
inc(i,1,ess){
int x=find(es[i].f),y=find(es[i].t);
if(x!=y)fa[x]=y,ans+=es[i].w,cnt++; if(cnt==n-1)break;
}
printf("%lld",ans); return 0;
}n头牛,每天牛都有体重与力量值。它们玩叠罗汉的游戏,每个牛的危险值等于它上面的牛的体重总和减去它的力量值,求所有方案中危险值最大的最小。
贪心。第i头牛比第j头牛高当且仅当i的重量-j的力量<j的重量-i的力量。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 50010
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct nd{int a,b;}; nd nds[maxn]; int n,sm,mx;
bool cmp(nd a,nd b){return a.a-b.b<b.a-a.b;}
int main(){
n=read(); inc(i,1,n)nds[i]=(nd){read(),read()}; sort(nds+1,nds+1+n,cmp); mx=-0x3fffffff;
inc(i,1,n){
mx=max(mx,sm-nds[i].b); sm+=nds[i].a;
}
printf("%d",mx); return 0;
}n个宝石,每个有重量和价值,要挂一些在手镯上,求满足总质量不超过m的最大总价值。n≤3402,m≤12880
01背包。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define dec(i,j,k) for(int i=j;i>=k;i--)
#define maxn 50100
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,f[maxn];
int main(){
n=read(); m=read();
inc(i,1,n){
int a=read(),b=read(); dec(j,m,a)f[j]=max(f[j],f[j-a]+b);
}
printf("%d",f[m]); return 0;
}有一个S串和一个T串,不断地在S串里匹配T串,然后将其删除。S串、T串长度≤1000000。
用1、2两个栈,每次将S串的当前字符压入1栈,当前匹配到T串的位置压入2栈,如果匹配出一个T串,则让1、2栈中匹配T串的子串出栈,然后令当前匹配到T串的位置变为2栈顶的数,匹配过程可以用KMP加速。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define maxn 1000010
#define inc(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
char s[maxn],t[maxn],st1[maxn]; int lens,lent,st2[maxn],top,fail[maxn];
void getfail(){
int j=0;
inc(i,2,lent){
while(j&&t[i]!=t[j+1])j=fail[j];
if(t[i]==t[j+1])j++; fail[i]=j;
}
}
int main(){
char ch=getchar(); while(ch<'a'||ch>'z')ch=getchar();
lens=0; while(ch>='a'&&ch<='z')s[++lens]=ch,ch=getchar();
ch=getchar(); while(ch<'a'||ch>'z')ch=getchar();
lent=0; while(ch>='a'&&ch<='z')t[++lent]=ch,ch=getchar();
getfail(); int j=0,top=0;
inc(i,1,lens){
while(j&&s[i]!=t[j+1])j=fail[j]; if(s[i]==t[j+1])j++;
st1[++top]=s[i],st2[top]=j;
if(j==lent){while(j)top--,j--; j=st2[top];}
}
inc(i,1,top)printf("%c",st1[i]); return 0;
}John要建一个奶酪塔,高度最大为T。他有N种奶酪,每种无限个,第i种高度为Hi(一定是5的倍数),价值为Vi。一块高度>=K的奶酪被称为大奶酪,一个奶酪如果在它上方有大奶酪(多块只算一次),它的高度就会变成原来的4/5。求最大价值。n≤100,t≤1000
可以枚举放哪个≥k的奶酪放在顶,其它奶酪高度变为4/5,做个完全背包。最后再算一个没有≥k的奶酪放在顶的最大价值,比较一下。注意被放在顶的奶酪可以再选,因为是每种奶酪无限个。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 110
#define INF 0x3fffffff
using namespace std;
struct nd{int h,v;}nds[maxn];
int f[2][maxn*10],n,t,k,x,y,ans;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int main(){
n=read(); t=read(); k=read(); inc(i,1,n)nds[i].v=read(),nds[i].h=read();
inc(i,1,n)if(nds[i].h>=k&&t>=nds[i].h){
x=0; y=1; memset(f,0,sizeof(f)); t-=nds[i].h;
for(int j=n;j>=1;j--){
for(int l=t;l>=0;l--){
if(l+nds[j].h/5*4>t)f[y][l]=f[x][l];else f[y][l]=max(f[y][l+nds[j].h/5*4]+nds[j].v,f[x][l]);
}
swap(x,y);
}
ans=max(ans,f[x][0]+nds[i].v); t+=nds[i].h;
}
x=0; y=1; memset(f,0,sizeof(f));
for(int i=n;i>=1;i--)if(nds[i].h<k){
f[y][t]=0;
for(int j=t;j>=0;j--){
if(j+nds[i].h>t)f[y][j]=f[x][j];else f[y][j]=max(f[y][j+nds[i].h]+nds[i].v,f[x][j]);
}
swap(x,y);
}
ans=max(ans,f[x][0]); printf("%d",ans); return 0;
return 0;
}约翰的N头奶牛站成一排,奶牛i的身高是Hi。对于奶牛i,如果奶牛j满足i<j且Hi<Hj,我们可以说奶牛i可以仰望奶牛j。求出每只奶牛离她最近的仰望对象。n≤100000.
用一个单调栈维护即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a[maxn],top,s1[maxn],s2[maxn],ans[maxn];
int main(){
n=read(); inc(i,1,n)a[i]=read(); top=1; s1[1]=0x3fffffff; s2[1]=0;
for(int i=n;i>=1;i--){
while(top&&a[i]>=s1[top])top--; ans[i]=s2[top]; s1[++top]=a[i]; s2[top]=i;
}
inc(i,1,n)printf("%d\n",ans[i]); return 0;
}n个数,如果其中两个数fi≤fj且fi≥0.9*fj,则它们要被比较。求多少对数要被比较。n≤100000。
排序然后双指针法。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,a[maxn],l,r; long long ans;
int main(){
n=read(); inc(i,1,n)a[i]=read(); sort(a+1,a+n+1);
l=1; r=1;
while(r<n){
r++; while(l<r&&a[l]+1e-8<a[r]*0.9)l++; ans+=r-l;
}
printf("%lld",ans); return 0;
}给一个序列和一个最大值,要求找一个最长连续子串,使里面任意两个数相差不超过这个最大值。序列大小≤3000000
用两个单调队列,分别维护当前区间的最大值和最小值,然后用双指针法。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 3000010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct nd{int v,pos;};
int n,a[maxn],k,l,r,ans,ql1,qr1,ql2,qr2; nd q1[maxn],q2[maxn];
int main(){
k=read(); n=read(); inc(i,1,n)a[i]=read();
l=1; r=1; ans=1; ql1=qr1=ql2=qr2=1; q1[1]=q2[1]=(nd){a[1],1};
while(r<n){
r++;
while(ql1<=qr1&&ql2<=qr2&&a[r]-q1[ql1].v>k){l++; if(l>q1[ql1].pos)ql1++; if(l>q2[ql2].pos)ql2++;}
while(ql1<=qr1&&ql2<=qr2&&q2[ql2].v-a[r]>k){l++; if(l>q1[ql1].pos)ql1++; if(l>q2[ql2].pos)ql2++;}
ans=max(ans,r-l+1);
while(ql1<=qr1&&a[r]<=q1[qr1].v)qr1--; q1[++qr1]=(nd){a[r],r};
while(ql2<=qr2&&a[r]>=q2[qr2].v)qr2--; q2[++qr2]=(nd){a[r],r};
}
printf("%d",ans); return 0;
}n个杯子排成一行,花费c_ij元,可以知道杯子i,i+1,…,j底下藏有球的总数的奇偶性。求问至少需要花费多少元才能保证猜出哪些杯子底下藏着球。
令杯子1..i的和为sum[i],那么当知道sum[i]和sum[i-1]即可推算出i下是否有球。故可以连边(i-1,j,c_ij),然后求最小生成树即可。注意点数会变为n+1,因为0也是点。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 2010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int f,t,w;}; e es[maxn*maxn]; int ess;
bool cmp(e a,e b){return a.w<b.w;}
int n,fa[maxn],cnt; long long ans;
int find(int x){
return x==fa[x]?x:fa[x]=find(fa[x]);
}
int main(){
n=read(); inc(i,1,n)inc(j,i,n){es[++ess]=(e){i-1,j,read()};}
sort(es+1,es+ess+1,cmp); inc(i,1,n)fa[i]=i;
inc(i,1,ess){
int x=find(es[i].f),y=find(es[i].t); if(x!=y)fa[x]=y,cnt++,ans+=es[i].w;
if(cnt==n)break;
}
printf("%lld",ans); return 0;
}初始时,一个有N枚硬币的堆栈放在地上,每枚硬币都有一个价值。开始玩游戏时,第一个玩家可以从堆顶拿走一枚或两枚硬币。之后每一轮中,当前的玩家至少拿走一枚硬币,至多拿走对手上一次所拿硬币数量的两倍。当没有硬币可拿时,游戏结束。 两个玩家都希望拿到最多钱数的硬币。求第一个玩家最多能拿多少钱。n≤2000。
首先有dp方程:f[i][j][0]=max(f[i][k][1]+sum(i-k,i)),1≤k≤min(j*2,i),f[i][j][1]=min(f[i][k][0]),1≤k≤min(j*2,i)。
然而这样会超时。发现所以f[i][k][1]的最大值实际上是f[i][j*2][1]、f[i][j*2-1][1]、f[i][j-1][0]的最大值,f[i][k][0]的最小值也是f[i][j*2][0]、f[i][j*2-1][0]、f[i][j-1][1]的最小值。故可以把dp优化到O(n^2)可过。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 2010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int a[maxn],sm[maxn],f[maxn][maxn][2],n;
int main(){
n=read(); inc(i,1,n)a[i]=read(); for(int i=n;i>=1;i--)sm[n-i+1]=sm[n-i]+a[i];
inc(i,1,n)
inc(j,1,n){
f[i][j][0]=j>1?f[i][j-1][0]:0; int k;
k=2*j-1; if(k<=i)f[i][j][0]=max(f[i][j][0],f[i-k][k][1]+sm[i]-sm[i-k]);
k=2*j; if(k<=i)f[i][j][0]=max(f[i][j][0],f[i-k][k][1]+sm[i]-sm[i-k]);
f[i][j][1]=j>1?f[i][j-1][1]:0x3fffffff;
k=2*j-1; if(k<=i)f[i][j][1]=min(f[i][j][1],f[i-k][k][0]);
k=2*j; if(k<=i)f[i][j][1]=min(f[i][j][1],f[i-k][k][0]);
}
printf("%d",f[n][1][0]); return 0;
}对一个01序列进行染色,每次能将一个区间染上色(可覆盖之前染的),共能染k次,求最大正确染色个数。n≤100000,m≤50。
结论:染k次最多能把序列分成2*k-1段。故dp即可:
f[i][j][0]=max(f[i+1][j+1][1]+a[i]==1,f[i+1][j][0]+a[i]==0)
f[i][j][1]=max(f[i+1][j][1]+a[i]==1,f[i+1][j+1][0]+a[i]==0)
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 110
#define INF 0x3fffffff
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,f[2][maxn][3],k,x,y; bool a[maxn*1000];
int main(){
n=read(); k=2*read()-1; inc(i,1,n)a[i]=read(); x=0; y=1;
for(int i=n;i>=1;i--){
f[x][k+1][0]=f[x][k+1][1]=-INF;
inc(j,1,k){
f[y][j][0]=max(f[x][j][0]+(a[i]==0),f[x][j+1][1]+(a[i]==1));
f[y][j][1]=max(f[x][j+1][0]+(a[i]==0),f[x][j][1]+(a[i]==1));
}
swap(x,y);
}
printf("%d",max(f[x][1][0],f[x][1][1])); return 0;
}n个人,任何两个认识的人不是朋友就是敌人,而且满足: 1、 我朋友的朋友是我的朋友; 2、 我敌人的敌人是我的朋友; 所有是朋友的人组成一个团伙。告诉你关于这n个人的m条信息,即某两个人是朋友,或者某两个人是敌人,求这个城市最多可能有多少个团伙。n≤1000,m≤5000。
每个点拆成两个。如果a和b是朋友,那么将a和b放入一个集合;如果是敌人,那么将a和b’放入一个集合以及a’和b放入一个集合,这样可以保证条件2。集合用并查集维护。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 1010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,fa[maxn*2],vis[maxn*2],ans; char opt[3];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
int main(){
n=read(); m=read(); inc(i,1,2*n)fa[i]=i;
inc(i,1,m){
scanf("%s",opt); int xx=read(),yy=read();
if(opt[0]=='F'){
int x=find(xx),y=find(yy); fa[x]=y;
}else{
int x=find(xx),y=find(yy+n); fa[x]=y;
x=find(xx+n),y=find(yy); fa[x]=y;
}
}
inc(i,1,n){int x=find(i); if(!vis[x])ans++,vis[x]=1;}
printf("%d",ans); return 0;
}n点m边双向图,问能否将一些边变成单向使得每个点只有一个入度。n≤100000,m≤200000。
结论:当图中每个点都与至少一个环相连时满足条件。故用并查集不断加边,如果两个顶点已在一个集合中,则将该集合根节点打标记,如果不在,若其中一个顶点所在集合被打了标记,则合并后的集合根节点也打标记。最后如果有集合没被打标记说明无法满足条件,否则可以满足。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 100010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
int n,m,fa[maxn],vis[maxn];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
int main(){
n=read(); m=read(); inc(i,1,n)fa[i]=i;
inc(i,1,m){
int x=find(read()),y=find(read());
if(x==y)vis[x]=1;else{
fa[x]=y; vis[y]|=vis[x];
}
}
inc(i,1,n)if(!vis[find(i)]){puts("NIE"); return 0;}
puts("TAK"); return 0;
}给个无向图和一个删点序列。求每次删完一个点后(将该点所连所有边也删掉)剩余联通块个数。点数≤400000。
离线,先将所有点删掉,然后将剩余的边两端点合并入一个联通块,接着按删点序列倒序加点,将删掉的边加下去,把加入的边两端点合并入一个联通块。注意每次加点总点数要加一。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define inc(i,j,k) for(int i=j;i<=k;i++)
#define maxn 400010
using namespace std;
inline int read(){
char ch=getchar(); int f=1,x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct e{int f,t,n;}es[maxn]; int ess,g[maxn];
void pe(int f,int t){
es[++ess]=(e){f,t,g[f]}; g[f]=ess; es[++ess]=(e){t,f,g[t]}; g[t]=ess;
}
int n,m,fa[maxn],cnt,k,a[maxn],ans[maxn],del[maxn];
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
void merge(int xx,int yy){int x=find(xx),y=find(yy); if(x!=y)fa[x]=y,cnt--;}
int main(){
n=read(); m=read(); inc(i,1,m)pe(read()+1,read()+1); k=read(); inc(i,1,k)del[a[i]=read()+1]=i;
inc(i,1,n)fa[i]=i; cnt=n-k;
inc(i,1,ess)if(!del[es[i].f]&&!del[es[i].t])merge(es[i].f,es[i].t); ans[k+1]=cnt;
for(int i=k;i>=1;i--){
cnt++; for(int j=g[a[i]];j;j=es[j].n)if(del[es[j].t]>i||!del[es[j].t])merge(a[i],es[j].t);
ans[i]=cnt;
}
inc(i,1,k+1)printf("%d\n",ans[i]); return 0;
}求两个正整数的积,每个数≤40位。
为什么C++不能支持高精度呢……